Poynting for Microwave 解析事例
負の屈折率を持つメタマテリアルプリズム
メタマテリアルとは
- 媒質は、その電磁気的特性(誘電率 ε、透磁率 μ)に応じて下図のように分類できる。
- 金属ワイヤや分割リングで微細構造を作ることにより、(ある周波数で)媒質の電気的特性はコントロールできる。
- そのような微細構造を持つ人工的な複合材料・物質は、「メタマテリアル」と呼ばれる。
- 特にDNG媒質の特性をもつメタマテリアルは、自然界にある通常の媒質にはない特性を実現できるため、近年、さまざまな分野で注目されている。
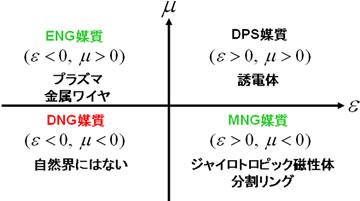
図1 媒質の分類
| DPS | double positive |
|---|---|
| ENG | epsilon-negative |
| MNG | mu-negative |
| DNG | double negative |
DNGメタマテリアルの代表例
分割リング(SRR)とワイヤの組合せ
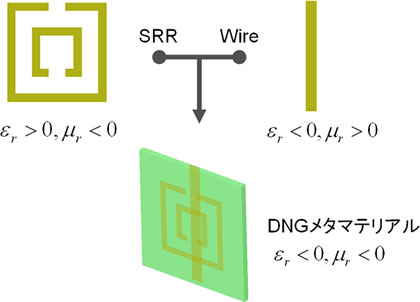
図2 DNGメタマテリアルの構成
DNGメタマテリアルの特徴
- 特定の周波数領域で ε と μ 両方が負⇒負の屈折率が実現できる。
- 応用例:プリズム、完全レンズ、Cloakingによる不可視化
- たとえば、負の屈折率を持つプリズムは下図のように振舞う。
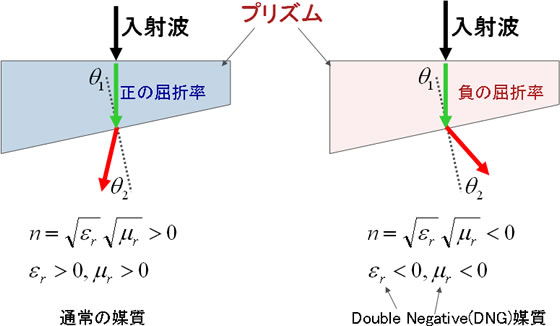
図3 通常媒質のプリズムとDNG媒質のプリズムの違い
Poynting GUIによるモデル化
SRR+ワイヤモデル1セル分の作成
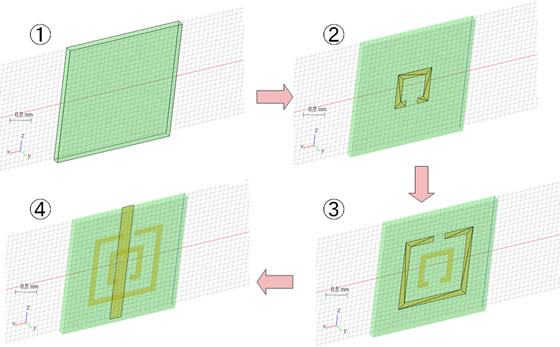
図4 作成手順
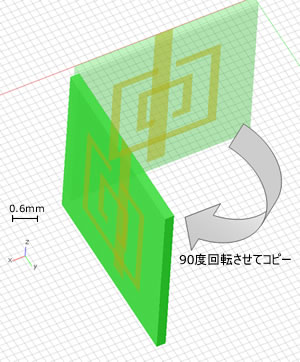
図5 SRR+ワイヤのコピー
プリズム形状の作成
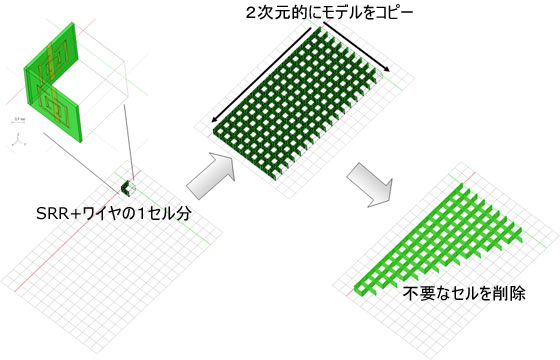
図6
解析モデル
負の屈折率を持つプリズムモデル
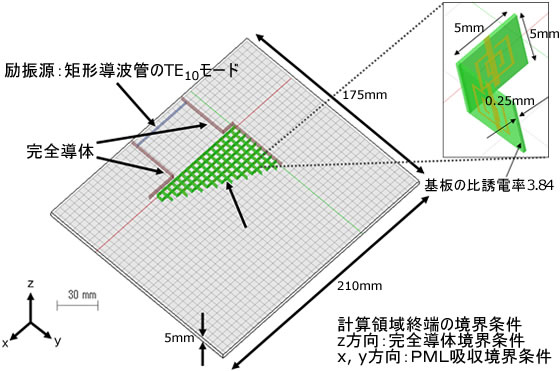
図7
数値波源:数値データを励振源の空間分布としてインポート可能
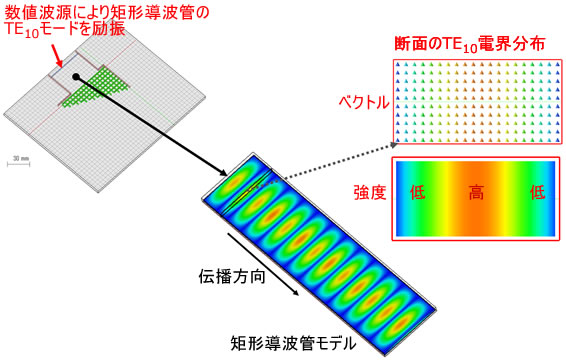
図8 矩形導波管を伝播するTE10モードと断面の電界分布
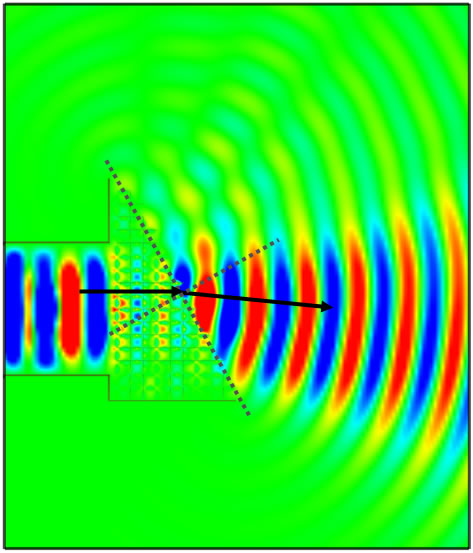
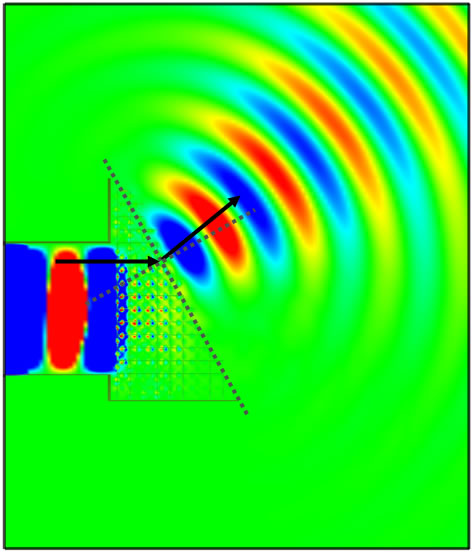
シミュレーション結果
正の屈折率
負の屈折率
まとめ
- PoyntingによるDNGメタマテリアルの電磁界シミュレーション
- 分割リング+ワイヤ型のメタマテリアルプリズムのモデリング
- 屈折現象の周波数依存性を確認
- 負の屈折率を再現
参考文献
- R. A. Shelby, D. R. Smith, S. Schultz, “Experimental verification of a negative index of refraction”, Science, vol..292, 2001, pp.77-79.
- R.A. Shelby, et.al., “Microwave transmission through a two-dimensional, isotropic, heft-handed metamaterial, Applied Physics Letter, Vol. 78, No. 4, 2001, pp.489-491.
- C. D. Moss, et. al., “Numerical Studies of left handed metamaterials”, Progress in electromagnetic research, PIER 35, pp.315-334, 2002.
- C. G. Parazzoli, et. al., “Experimental verification and simulation of negative index of refraction using Snell’s law”, Physical Review Letters, vol.90, no.10, 2003.
- D. R. Smith, et.al., “Electromagnetic parameter retrieval from inhomogeneous metamaterial, Physical Review, vol.71, 036617, 2005.
- N. Engheta, R.W. Ziolkowski, “Metamaterials: Physics and Engineering Explorations”, Wiley-IEEE Press, 2006.