Poynting for Optics 解析事例
散乱解析
Poyntingを用いた散乱解析事例として、Mie散乱[1]を紹介します。
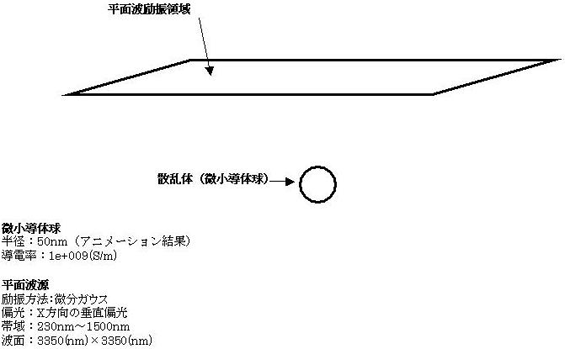
図1 計算モデル
微小導体球に対して、十分広い平面励振波源を用意します。この励振波源から直線偏波で振動するパルス波を発生させ、微小導体球に入射させることによって、散乱波を生じさせます。

図2 入射波+散乱波

図3 散乱波
微小導体球にパルス波を入射させたときのアニメーションです。散乱波は、微弱であるために図2から観測することは難しいですが、 散乱に寄与していない電磁波を取り除くことで、図3のようなリング状に広がる散乱波を観測することができます。[2]
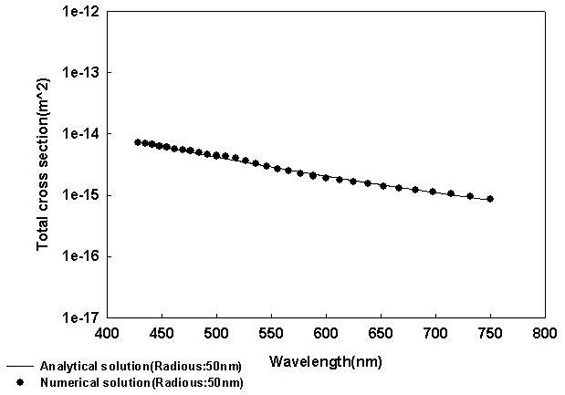
図4 全散乱断面積の解析解と数値解との比較
Mie散乱の全散乱断面積の解析解と、Poyntingで計算した全散乱断面積[3]の数値解とを比較したグラフです。 400nm~750nmの帯域に渡り、良好な一致を示しています。
[1] Mieが、電磁波が波長と同程度の球状物体に当たったときの散乱についての解析的な研究成果を発表したもの。
[2] ここでは反射も広義の意味で、散乱に含むものとします。
[3] (θ、Φ)方向の散乱断面積を極座標上のすべて方向で積分したものを表します。