データの幾何学的構造を活用する新しい機械学習
パラダイムStratification Learningを開発

製品設計プロセスの効率化や革新的デザインの自動発見などに期待

2020年2月4日

開発の背景

理研AIP-富士通連携センターでは、多目的最適化問題*1 (図1) の解を効率よく近似するための学習技術の研究を行っています。従来、多目的最適化問題の解を近似するための手法として応答曲面法などがありましたが、これらの手法は解集合の幾何学的構造 (滑層) をとらえることができず、多くの訓練データ（最適化計算）が必要でした。

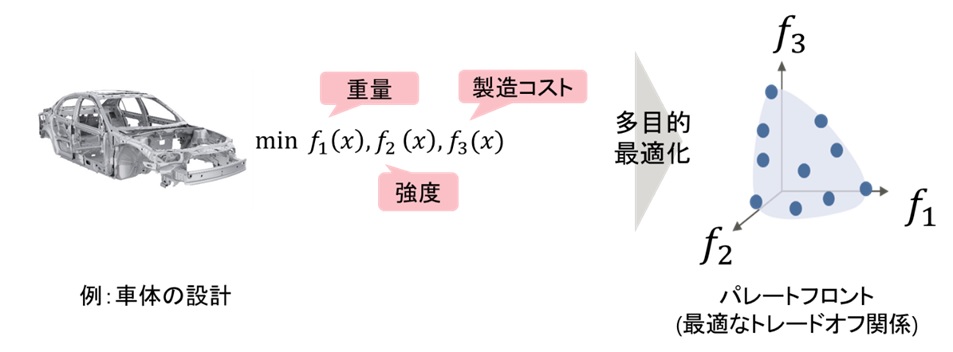図1　多目的最適化のイメージ

技術の特徴

この課題を解決するため、理研AIP-富士通連携センターではベジエ単体*2(図2)を用いた解集合の近似手法を開発し，昨年の国際会議 AAAI-19 で発表しました*3。 この研究では本技術が従来よりも少ない訓練データで精度よく近似できることを実験的に示していましたが，その近似精度について理論的な保証はなく、どの程度学習に必要なデータ数を削減できるかわかっていませんでした。

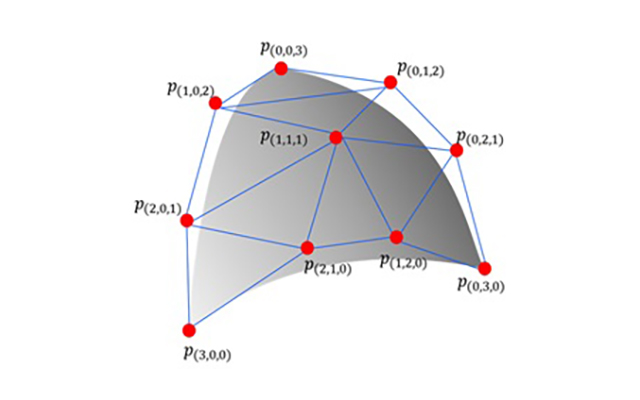
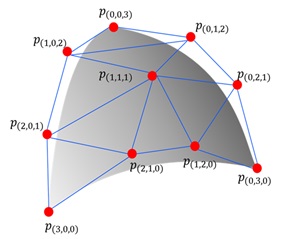図2　ベジエ単体

ベジエ単体には、一様抽出に基づく近似法と層化抽出(図3)に基づく近似法があります。本研究では、これらの手法の近似精度を統計的漸近論に基づいて解明しました。その結果、真の解集合が2次のベジエ単体で表される場合、層化抽出を行うことで、およそ半数（約57.4%）の訓練データで一様抽出と同等の精度を達成できることができることがわかりました。

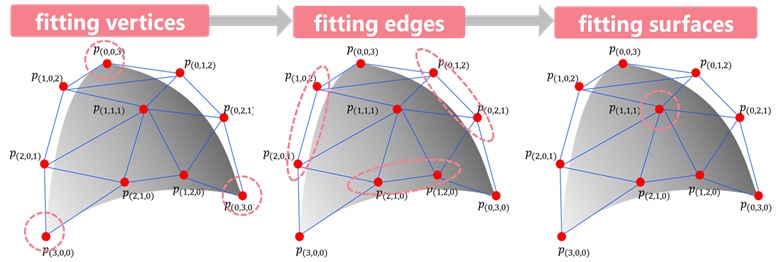図3　層化抽出に基づく学習法

今後

本技術は、訓練データ（その生成には実験やシミュレーションを伴う高コストな最適化計算が必要）を削減することにより、製品設計プロセスを効率化します。さらに、多様な設計案を網羅することができるため、人手による試行錯誤では思いもしなかったような革新的なデザインを自動発見することも期待できます。今後ビジネス課題を対象とした実証実験を進めていく予定です。また製品設計以外にも、施設配置問題やスパースモデリングなどの様々な課題への応用も期待されています。

関連情報

本技術は人工知能分野で最も権威のある国際会議の一つであるAAAI-20に採択されました。

• 学会名

  34th AAAI Conference on Artificial Intelligence (AAAI-20)
  ※AAAI-20プログラム

• 開催日

  2020年2月7日～2月12日

• 開催場所

  アメリカ　ニューヨーク

• タイトル

  Asymptotic Risk of Bézier Simplex Fitting

• 著者

  田中 章詞（理研 AIP，慶應義塾大学）、三内 顕義（理研 AIP，慶應義塾大学）
  小林 健 （富士通研究所，理研AIP，東京工業大学）、濱田 直希 （富士通研究所，理研AIP）
  ※プレプリント　※プログラム

注釈

*1　多目的最適化問題：複数の目的関数（評価指標）を同時に最適化する問題。

*2　ベジエ単体：コンピュータグラフィックスの分野で用いられるベジエ曲線を高次元に一般化したもの。

*3　Ken Kobayashi, Naoki Hamada, Akiyoshi Sannai, Akinori Tanaka, Kenichi Bannai, and Masashi Sugiyama, Bézier Simplex Fitting: Describing Pareto Fronts of Simplicial Problems with Small Samples in Multi-Objective Optimization, in Proceedings of the AAAI Conference on Artificial Intelligence, 33(1), 2304-2313 (2019). https://doi.org/10.1609/aaai.v33i01.33012304

本件に関するお問合せ

fj-stratification@dl.jp.fujitsu.com

EEA (European Economic Area) 加盟国所在の方は以下からお問い合わせください。
Ask Fujitsu
Tel: +44-12-3579-7711
http://www.fujitsu.com/uk/contact/index.html

Fujitsu, London Office
Address :22 Baker Street
London United Kingdom
W1U 3BW

付録

理研AIP-富士通連携センターが開発したStratification Learningは、データ空間の滑層分割 (stratification) という幾何学的構造を活用することで、高次元の現象をごく僅かなデータから高精度に推測する機械学習パラダイムです。データ空間の構造を活用した機械学習パラダイムとしては、多様体学習 (manifold learning) が有名です。多様体学習では、高次元データはしばしばスパースで、何らかの低次元多様体に沿って分布していると想定します。多様体構造に注目することで、高次元の現象を驚くほど少ないデータで推測することができます。Stratification Learningでは、高次元データはある低次元滑層分割集合 (stratified set) に沿って分布していると想定します。滑層分割集合は、様々な次元の多様体を貼り合わせて作られる図形で、1つの多様体では表せない複雑な形状を表現できます。加えて、各データ点はいずれかの滑層 (stratum)、すなわち滑層分割集合の構成要素となる多様体に属するものとして層別化されていると想定します。これらの追加情報によって、さらなる学習の効率化を狙うわけです。
　Stratification Learningにはどんな応用があるのでしょうか？このようなデータが現れる典型的な事例として、多目的最適化が挙げられます。ある緩い条件のもとで、ほとんどすべての多目的最適化問題の解集合は滑層分割集合をなすことが知られています（無制約最適化の場合は1977年の研究*4で、制約付き最適化の場合は1978年の研究*5で示されています）。多目的最適化は、産業・科学のあらゆる場面で現れる問題です。たとえば製品設計では、性能・コスト・安全性などの複数の目的関数を最適化する多目的最適化問題に直面します。この解集合を求めることで、これらの目的関数のトレードオフが明らかになり、製品をどのように設計すべきかについて様々な知見が得られます。しかし、設計案の評価には実験や計算機シミュレーションが伴い、多大な時間と費用がかかるため、実用上は多くの解（設計案）を求めることはできません。評価した少数の解に基づいて、解集合全体を推定する必要があります。
　理研AIP-富士通連携センターでは、製品設計の多目的最適化において頻繁に現れる問題クラスである、単体的な問題に注目しました。単体的な問題では、解集合は単体（2目的ならば線分、3目的ならば三角形、4目的ならば四面体、N目的ならばN-1次元単体）と同相で、単体の面は一部の目的関数を最適化する部分問題の解集合に相当します。このような図形は、滑層分割集合の最もシンプルな例といえます。最適化する目的関数を入れ替えてそれぞれの部分問題を解くことによって、解集合のそれぞれの滑層から解を層化抽出することができます。昨年の研究*3では、単体的な問題の解集合はベジエ単体によって任意の精度で近似できることを示しました。加えて、上記の層化抽出が一様抽出に比べて近似精度を高めることを実験的に示しました。しかし、この実験結果に対する理論的な裏付けはありませんでした。
　今回の研究では、一様抽出と層化抽出の違いが近似精度に与える影響を統計的漸近論に基づいて解明しました。その結果、7目的最適化問題において真の解集合が2次のベジエ単体で表される場合、層化抽出を行うことで、およそ半数（約57.4%）の訓練データで一様抽出と同等の精度を達成できることができることがわかりました。目的数が増えると、両者の差はさらに大きくなります。一方で、この差は最適化問題の設計変数の数には依存しないことから、解集合の内在的次元にのみ依存していることもわかりました。
　本技術は、実際に評価した少数の解（設計案）をもとに解集合（設計案全体）を網羅的に求めることを可能とするものです。評価回数削減によるコストダウンに加えて、設計案の網羅的探索により、人手による試行錯誤では思いもしなかったような革新的設計を発見することが期待できます。なお、最近の研究*6によって、ほとんどすべての強凸最適化問題は単体的な問題であることも示されました。これは応用において単体的な問題が頻出することを理論的に裏付けるものと考えられます。製品設計以外にも、施設配置問題やスパースモデリングなどは、ある種の問題の構造を保つ変換によって強凸多目的最適化問題に変換できるため、本技術の応用が期待できます。より一般的な最適化問題の解集合も、強凸多目的最適化問題の解集合の貼り合わせとして表現できることがあります。したがって、今回の研究成果は、より幅広い最適化問題を扱うための足掛かりとなることも期待できます。

*4　Yieh-Hei Wan, On the Algebraic Criteria for Local Pareto Optima. I, Topology 16(1), 113-117 (1977). https://doi.org/10.1016/0040-9383(77)90035-0

*5　Yieh-Hei Wan, On the Algebraic Criteria for Local Pareto Optima. II, Transactions of the American Mathematical Society 245, 385-397 (1978). https://doi.org/10.1090/S0002-9947-1978-0511417-1

*6　Naoki Hamada, Kenta Hayano, Shunsuke Ichiki, Yutaro Kabata, and Hiroshi Teramoto, Topology of Pareto sets of strongly convex problems, arXiv:1904.03615 [math.OC] (2019). https://arxiv.org/abs/1904.03615