Archived content
NOTE: this is an archived page and the content is likely to be out of date.
Fujitsu Develops High-speed Learning Technology for Deep Neural Networks
Fujitsu Research & Development Center Co. Ltd.
Fujitsu R&D Center Co., Ltd. (FRDC) announced the development of a high-speed learning technology applicable to the Deep Neural Network (DNN). This technology can effectively reduce the complexity and the size of Deep Neural Network model by using regularization strategy. Moreover, the developed technology uses the quadratic approximation method to determine the optimum path for the DNN model to be converged, thereby improving the speed of learning the DNN model. With this technology, the learning time spent on building a DNN model can be reduced by 50%. It is a general optimization technology applicable to the entire field of machine learning, and can be widely used in various application scenarios.
[Development Background]
As an important elementary technologies of artificial intelligence (AI), the deep learning technology has been successfully applied in many fields after its breakthrough in recent years. However, implementing a high performance Deep Neural Network model often requires massive training data and complex model structure, which leads to heavy computation cost and long computation time. In speech recognition field, for example, a practical DNN model is usually composed by tens of thousands of neurons, and thousands of hours of speech data is needed to train such a complex model, which takes days or even dozen of days.
Due to the complexity of the DNN model, the effective learning method has become an important cornerstone for the practical use of the deep learning technology.
[Issue]
The Deep Neural Network model is characterized by two parts: the network structure and network parameters. The network structure is determined by the number of network layers, amount of neurons in each layer, as well as the style that the neurons are connected; while the network parameters refer to the connection weights between the neurons. When the network structure is fixed, learning a neural network is in essence to find the optimum network parameter values, viz. the "knowledge" learned by the neural network through the learning process is covered by the network parameters, e.g., the connection weights.
A DNN model generally has too many (million-level or more) parameters, so, the optimum parameter values are impossible to be directly determined. In fact, we can only rely on some optimization strategy to find the approximate optimum parameter values through an iteration procedure.
Linear approximation, e.g. stochastic gradient descent, is the commonly used learning method for Deep Neural Network, which uses the gradient direction information to guide the DNN model iteratively toward the optimum position. However, low convergence speed is usually resulted due to the inherent zig-zag optimization path in linear approximation strategy, as shown in Fig.1. The quadratic approximation methods, e.g. Newton's gradient descent, can realize convergence along the shortest path, but, it cannot be directly used due to the heavy computation cost in the high-dimensional space.
[About Technology]
- Quadratic Approximation based Learning
FRDC develops the PROXTONE (PROXimal sTOchastic NEwton-type gradient descent) method to get the optimum Deep Neural Network parameter values by the learning process. This method utilizes both the curvature and the gradient information to construct the regularized quadratic function in iterative optimization, thus, reduces the iteration epochs and accelerates the convergence speed.
The iterative optimization is just like finding the shortest way to reach the bottom of a valley. Imagining that you are selecting the walking direction at current site, the quadratic approximation method will consider not only whether the slope of the current site is large enough, but also whether the slope where you have moved a further step is still large enough, i.e. more far-sighted, as shown in Fig.1.
Fig.1 Comparison of Linear Approximation and Quadratic Approximation Optimization
- Reduce Computational Complexity by Using Low-Dimensional Space
The quadratic approximation method can effectively reduce the iteration epochs, but this is achieved at the cost of more computations in each epoch, due to the massive matrix operations required in quadratic approximation method, especially the matrix inverse operation. When the number of parameters to be determined in the neural network is too large, the matrix inverse operation will be most time-consuming.
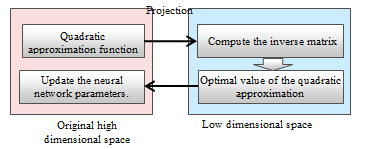
To improve the computational efficiency, our technology projects the quadratic approximation function from the high dimensional space (million-level parameter space) to a lower dimensional one (several hundred dimensions) in each iteration, where the inverse matrix is computed and the quadratic approximation function is solved. Then, the computed results are projected back to the original space to update the parameter values of the Deep Neural Network model, as shown in Fig.2.
Fig. 2 Low-Dimensional Space projection
- Sparsity
The regularization technique is adopted in the Deep Neural Network learning to ensure the sparsity of the DNN model, so as to reduce the size of the model.
[Effects]
Fig. 3 illustrates the result of building a DNN model by different learning methods. The DNN model is composed by 4 layers, and it is trained to realize the character recognition function on the benchmark MNIST dataset (10 categories, 50K training samples in this dataset). It is revealed from the handwritten character recognition application that the developed Deep Neural Network learning technology (PROXTONE in Fig.3) can reduce the learning time of the model by at least 50%.
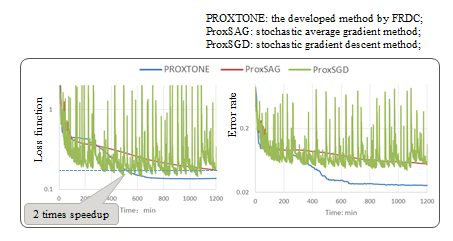
Fig. 3 DNN model learning by different methods
[Future plans]
Fujitsu R&D Center plans to further improve the performance of the learning technology along the direction of higher speed and smaller DNN model size, and aims to bring this technology into Fujitsu’s AI business after verifying its effectiveness in different types of deep neural network.
Contacts
![]() E-mail: multimedia@cn.fujitsu.com
E-mail: multimedia@cn.fujitsu.com
Company:Fujitsu R&D Center Co., Ltd.
Information Technology Lab.
Press Release ID: 2016-11-22
Date: 22 November, 2016
City: Beijing, China
Company:
Fujitsu Research and Development Center Co., Ltd.